Dinámica de Sistemas 4: mayo 2022

Mapeo del plano s al z y viceversa

En vista de que las variables complejas $s$ y $z$ están relacionadas mediante $z=e^{Ts}$ , la localización de los polos y los ceros en el plano $z$ está relacionado con la localización de los polos y ceros del plano $s$ . Por lo tanto, la estabilidad del sistema en lazo cerrado en tiempo discreto lineal e invariante con el tiempo puede determinarse con base en las posiciones de los polos de la función de transferencia pulso en lazo cerrado. Debe observarse que el comportamiento dinámico del sistema de control en tiempo discreto depende del período de muestreo $T$ .

Correspondencia del semiplano izquierdo del plano s hacia el plano z

Cuando en el proceso se incorpora un muestreo por impulsos, las variables complejas $z$ y $s$ quedan relacionadas mediante la ecuación:

$z=e^{Ts}$

Esto significa que un polo en el plano s puede quedar localizado en el plano $z$ mediante la transformación $z=e^{Ts}$ . Dado que la variable compleja $s$ está formada de una parte real σ y una parte imaginara ω, tenemos:

$s = \sigma +j\omega$

$\displaystyle z=e^{Ts}=e^{T(\sigma+j\omega)} =e^{T\sigma} e^{j(T\omega)} = e^{T\omega} e^{j(T\omega+2\pi k)}$

En esta última ecuación se observa que los polos y los ceros en el plano $s$ , donde las frecuencias difieren en múltiplos enteros de la frecuencia de muestreo $\displaystyle \omega_s = \frac{2\pi}{T}$ , corresponden a las mismas localizaciones en el plano $z$ . Esto significa que por cada valor de $z$ existirá un número infinito de valores $s$ .

Dado que σ es negativo en el semiplano izquierdo del plano $s$ , eso corresponde a:

$|z| = e^{T\sigma} < 1$

El eje $j\omega$ en el plano $s$ corresponde a $|z|=1$ .

Técnica del lugar de las raíces

El Lugar de las Raíces se define como el lugar geométrico que recorren los polos de un sistema en lazo cerrado cuando el valor de la ganancia proporcional K de su correspondiente función de transferencia en lazo abierto varía de 0 a +∞. Relacionado con este concepto, si dicha ganancia varía de 0 a -∞ el lugar geométrico recorrido por los polos del lazo cerrado recibe el nombre de Lugar Inverso de las Raíces. Así mismo, si es otro parámetro diferente a K el que varía de 0 a +∞ (o de 0 a -∞) se denomina Contorno de las Raíces o Lugar de las Raíces Generalizado (Contorno Inverso de las Raíces o Lugar Inverso de las Raíces Generalizado) a la trayectoria seguida por los polos.

Dado el sistema de la Figura 9.2, los polos en lazo cerrado satisfacen la ecuación característica:

Figura 9.2:

Diagrama de bloques de un sistema realimentado general

Es decir, un punto s₀ del plano complejo para que sea polo del lazo cerrado ha de cumplir dicha ecuación. Ya que s es una variable compleja, la ecuación anterior se puede desdoblar en las siguientes:

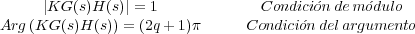$|KG (s)H (s)| = 1 Condici´onde m´odulo Arg (KG (s)H (s)) = (2q+ 1)π Condici´on delargumento$ (9.3)

por lo que el punto s₀ es polo del sistema en lazo cerrado si satisface ambas condiciones. Notad que ambas condiciones están referidas a la función de transferencia de lazo abierto del sistema.

En el contexto del Lugar de las Raíces el parámetro K es positivo y, por tanto, la condición del argumento queda simplificada a la expresión:

$Arg (G(s)H(s)) = (2q+ 1)π Condici´on delargumento$ (9.4)

ya que el argumento de un número real positivo es nulo. Entonces, dicha condición únicamente depende de la variable s y bastará, por lo tanto, con realizar la comprobación de si el punto en cuestión s₀ cumple la condición del argumento para determinar si dicho punto es polo del sistema en lazo cerrado para algún valor positivo de K. En caso afirmativo, mediante la condición del módulo se podrá conocer el valor concreto de la ganancia proporcional K para la cual el punto s₀ es raiz de la ecuación característica. Es decir, los puntos del plano complejo que satisfacen la condición del argumento son polos del sistema para algún valor positivo de K, y por lo tanto, pertenecen al Lugar de las Raíces.

Polos Dominantes

Los polos de la transferencia de un sistema que están más próximos al eje imaginario son los que determinan generalmente la respuesta transitoria

Para que un polo de la función de transferencia sea no dominante pueden ocurrir dos situaciones:

-Que la parte real del polo sea al menos 10 veces mayor que parte real del polo de baja frecuencia más cercano.

-Que haya un cero muy próximo a la ubicación del polo.

Efecto de los ceros

El cero en el área de control en una función de transferencia de un sistema puede ser interpretado como una «transferencia nula» entre la entrada y la salida del sistema en la frecuencia del propio cero. Esto quiere decir que si excitamos el sistema justo en la frecuencia del cero, esta no se verá reflejada en la respuesta del sistema.

O sea, de forma general si tenemos un sistema dado por:

Implica que tenemos un Cero en $s=-6$ y dos Polos en $s=-5$ y $s=-7$ .

Esto quiere decir que si a ese sistema, le colocamos una entrada de $u=e^{-6t}$ que en el dominio de laplace equivale a $U(s)=\dfrac{1}{s+6}$ , por lo tanto la respuesta del sistema viene dado por: