El Lugar de las Raíces se define como el lugar geométrico que recorren los polos de un sistema en lazo cerrado cuando el valor de la ganancia proporcional K de su correspondiente función de transferencia en lazo abierto varía de 0 a +∞. Relacionado con este concepto, si dicha ganancia varía de 0 a -∞ el lugar geométrico recorrido por los polos del lazo cerrado recibe el nombre de Lugar Inverso de las Raíces. Así mismo, si es otro parámetro diferente a K el que varía de 0 a +∞ (o de 0 a -∞) se denomina Contorno de las Raíces o Lugar de las Raíces Generalizado (Contorno Inverso de las Raíces o Lugar Inverso de las Raíces Generalizado) a la trayectoria seguida por los polos.
Dado el sistema de la Figura 9.2, los polos en lazo cerrado satisfacen la ecuación característica:| Figura 9.2: | Diagrama de bloques de un sistema realimentado general |
por lo que el punto s0 es polo del sistema en lazo cerrado si satisface ambas condiciones. Notad que ambas condiciones están referidas a la función de transferencia de lazo abierto del sistema.
En el contexto del Lugar de las Raíces el parámetro K es positivo y, por tanto, la condición del argumento queda simplificada a la expresión:
ya que el argumento de un número real positivo es nulo. Entonces, dicha condición únicamente depende de la variable s y bastará, por lo tanto, con realizar la comprobación de si el punto en cuestión s0 cumple la condición del argumento para determinar si dicho punto es polo del sistema en lazo cerrado para algún valor positivo de K. En caso afirmativo, mediante la condición del módulo se podrá conocer el valor concreto de la ganancia proporcional K para la cual el punto s0 es raiz de la ecuación característica. Es decir, los puntos del plano complejo que satisfacen la condición del argumento son polos del sistema para algún valor positivo de K, y por lo tanto, pertenecen al Lugar de las Raíces.

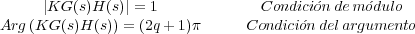 (9.3)
(9.3) (9.4)
(9.4)


No hay comentarios:
Publicar un comentario